reference:傻子都能看懂的并查集入门
简介
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
顾名思义就是有“合并集合”和“查找集合”两种操作的关于数据结构的一种算法。
性质
并查集算法不支持分割一个集合。
算法思想
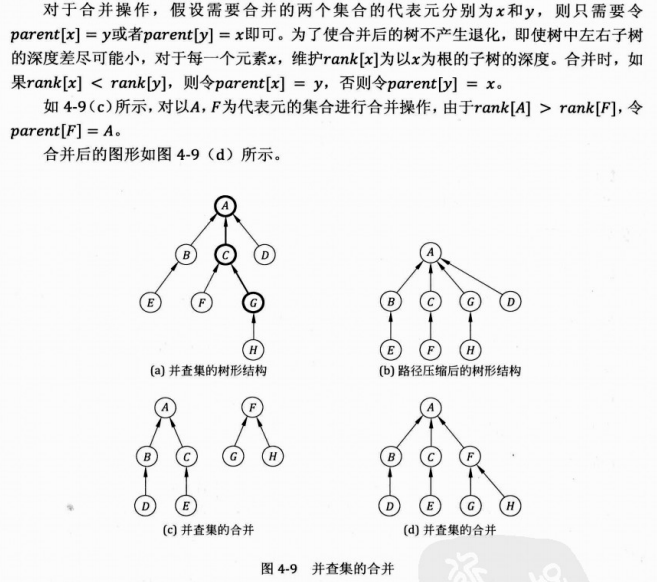
用集合中的某个元素来代表这个集合,该元素称为集合的代表元。
一个集合内的所有元素组织成以代表元为根的树形结构。
对于每一个元素 parent[x]指向x在树形结构上的父亲节点。如果x是根节点,则令parent[x] = x。
对于查找操作,假设需要确定x所在的的集合,也就是确定集合的代表元。可以沿着parent[x]不断在树形结构中向上移动,直到到达根节点。
判断两个元素是否属于同一集合,只需要看他们的代表元是否相同即可。
路径压缩
每次查找的时候,如果路径较长,则修改信息,以便下次查找的时候速度更快。
为了加快查找速度,查找时将x到根节点路径上的所有点的parent设为根节点,该优化方法称为压缩路径。
使用该优化后,平均复杂度可视为Ackerman函数的反函数,实际应用中可粗略认为其是一个常数。
用途
1、维护无向图的连通性。支持判断两个点是否在同一连通块内,和判断增加一条边是否会产生环。
2、用在求解最小生成树的Kruskal算法里。
初始化
初始化的时候,一个集合的parent都是这个集合自己的标号。没有跟它同类的集合,那么这个集合的源头只能是自己了。
在每一个单个的集合里面,有三个东西。
1,集合所代表的数据。(这个初始值根据需要自己定义,不固定)
2,这个集合的层次通常用rank表示(一般来说,初始化的工作之一就是将每一个集合里的rank置为0,以点为根的子树的深度)。
3,这个集合的类别parent(有的人也喜欢用set表示)(其实就是一个指针,用来指示这个集合属于那一类,合并过后的集合,他们的parent指向的最终值一定是相同的。)
结构体表示法
有的人是建立一个结构体把集合表示出来,如:
#define MAX 10000
struct Node
{
int data;
int rank;
int parent;
}node[MAX];
数组表示法
有的人则是弄很多相同大小的数组,如:
int set[max];//集合index的类别,或者用parent表示
int rank[max];//集合index的层次,通常初始化为0
int data[max];//集合index的数据类型
//初始化集合
void Make_Set(int i)
{
set[i]=i;//初始化的时候,一个集合的parent都是这个集合自己的标号。没有跟它同类的集合,那么这个集合的源头只能是自己了。
rank[i]=0;
}
一般来说,题目简单用数组,题目复杂用结构体,因为结构体有条理,数组可以少打几个字。
查找函数
就是找到parent指针的源头,可以把函数命名为get_parent(或者find_set)
如果集合的parent等于集合的编号(即还没有被合并或者没有同类),那么自然返回自身编号。
如果不同(即经过合并操作后指针指向了源头(合并后选出的rank高的集合))那么就可以调用递归函数:1
2
3
4
5
6
7
8
9
10
11/**
*查找集合i(一个元素是一个集合)的源头(递归实现)。
如果集合i的父亲是自己,说明自己就是源头,返回自己的标号;
否则查找集合i的父亲的源头。
**/
int get_parent(int x)
{
if(node[x].parent==x)
return x;
return get_parent(node[x].parent);
}
数组的话就是:1
2
3
4
5
6
7
8
9//查找集合i(一个元素是一个集合)的源头(递归实现)
int Find_Set(int i)
{
//如果集合i的父亲是自己,说明自己就是源头,返回自己的标号
if(set[i]==i)
return set[i];
//否则查找集合i的父亲的源头
return Find_Set(set[i]);
}
合并集合函数
1 | void Union(int a,int b) |
再给出数组显示的合并函数:1
2
3
4
5
6
7
8
9
10
11
12void Union(int i,int j)
{
i=Find_Set(i);
j=Find_Set(j);
if(i==j) return ;
if(rank[i]>rank[j]) set[j]=i;
else
{
if(rank[i]==rank[j]) rank[j]++;
set[i]=j;
}
}
实战
Description
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。 规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。如果x,y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
Input
第一行:三个整数n,m,p,(n< =5000,m< =5000,p< =5000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。 以下m行:每行两个数Mi,Mj,1< =Mi,Mj< =N,表示Mi和Mj具有亲戚关系。 接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。
11 8 6
1 2
1 3
2 4
5 6
5 7
6 8
7 9
10 11
4 6
3 9
5 9
11 6
7 8
3 4
Output
P行,每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
No
No
Yes
No
Yes
Yes
分析
初步分析觉得本题是一个图论中判断两个点是否在同一个连通子图中的问题。对于题目中的样例,以人为点,关系为边,建立无向图。
用图的数据结构的最大问题是,我们无法存下多至(M=)2 000 000条边的图,后面关于算法时效等诸多问题就免谈了。
用图表示关系过于“奢侈”了。其实本题只是一个对分离集合(并查集)操作的问题。
我们可以给每个人建立一个集合,集合的元素值有他自己,表示最开始时他不知道任何人是它的亲戚。以后每次给出一个亲戚关系a, b,则a和他的亲戚与b和他的亲戚就互为亲戚了,将a所在集合与b所在集合合并。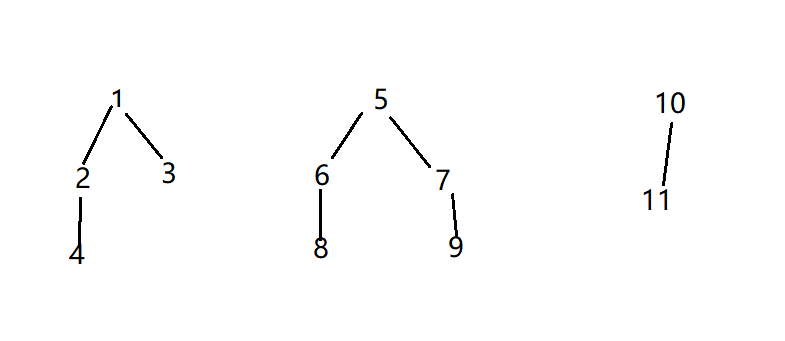
对于样例数据的操作全过程如下:
输入关系 分离集合
初始状态
(2,4) {2,4}
(5,7) {2,4} {5,7}
(1,3) {1,3} {2,4} {5,7}
(6,8) {1,3} {2,4} {5,7} {6,8}
(1,2) {1,2,3,4} {5,7} {6,8}
(5,6) {1,2,3,4} {5,6,7,8}
(7,9) {1,2,3,4} {5,6,7,8,9}
(10,11) {1,2,3,4} {5,6,7,8,9} {10,11}
最后我们得到3个集合{1,2,3,4}, {5,6,7}, {8,9},于是判断两个人是否亲戚的问题就变成判断两个数是否在同一个集合中的问题。如此一来,需要的数据结构就没有图结构那样庞大了。
算法需要以下几个子过程:
(1) 开始时,为每个人建立一个集合SUB-Make-Set(x);
(2) 得到一个关系后a,b,合并相应集合SUB-Union(a,b);
(3) 此外我们还需要判断两个人是否在同一个集合中,这就涉及到如何标识集合的问题。我们可以在每个集合中选一个代表标识集合,因此我们需要一个子过程给出每个集合的代表元SUB-Find-Set(a)。于是判断两个人是否在同一个集合中,即两个人是否为亲戚,等价于判断SUB-Find-Set(a)=SUB-Find-Set(b)。
并查集的“路径压缩”算法:在集合的查找过程中顺便将树的深度降低。采用路径压缩后,每一次查询所用的时间复杂度为增长极为缓慢的ackerman函数的反函数——α(x)。对于可以想象到的n,α(n)都是在5之内的。
CODE
1 |
|
